VI. ACCELERATION AND VELOCITY IN TERMS OF X
1. For a particle moving on the x-axis, the velocity at time t is given by:
(i) 
(ii) 
(iii) 
In each case, starting with 
, express t in terms of x, given that t=0 when x=1.
2. For a particle moving on the line x'Ox, the acceleration at time t is given by:
(i) 
(ii) 
(iii) 
In each case, using the result 
express v2 in terms of x given that v=0 when x=0.
3. A particle starts at the origin and moves along the x-axis in such a way that its velocity at (x,0) is given by dx/dt = cos2px. How long will it take to tranverse the distance from the origin to the point x=1/4? Will it ever reach the point x=1/2? Why?
4. The acceleration of a particle P moving along the x-axis is given by 
. If the particle starts from rest at x=5, find the velocity of P when it first reaches x=3.
5. The equation giving the acceleration of a body moving on the x-axis is 
, where x is the displacement at time t. If when t=0, x=1, dx/dt=2 (and dx/dt >0 for the motion) find an expression for v in terms of x and show that 
.
6. Prove that 
. The acceleration of a particle moving in a straight line and starting from rest at unit distance on the positive side of the origin, is given by (in the usual notation) by the equation 
. Calculate v when x=e2.
7. The velocity v of a point P is given by the formula 
and v=0 when x=0.
(i) At what other displacement from the origin is v=0.
(ii) What is the greatest value of v and where does this value occur ?
8. A particle initially at rest at the origin moves so that its velocity v is determined by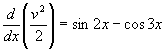 
. Find an expression for v2 in terms of x and hence determine the value of v when x=p/2.
9. (i) With the usual notation, prove that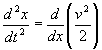 
.
(ii) A particle moves along the x-axis under the influence of a force so that its acceleration at any point on the line is directed towards 0 and varies inversely as the square of its distance from 0, i.e. 
where k is a constant. If it starts from rest at a distant of 3m on the positive side of 0 and is accelerating at 16 m/s2 towards 0, find its velocity when it is 2 m from 0.
10. (i) Find 
and 
in simplest forms.
(ii) Two bodies P and Q are travelling towards O on the x-axis, so that their respective velocities at a distance x cm from 0 are 
Initially they are both 5 cm from 0; find the times for each body to reach 0.
11. A particle moves along the x-axis. When it is distant x from the origin 0, it is acted upon by a restoring force directed towards 0; this force produces an acceleration proportional to the cube of the distance i.e. 
, where k is a constant. If when x=1, 
, 
, show that 
and that the particle never moves outside a certain interval. What is this interval.
12. The acceleration of a particle moving in a straight line is given by 
. If v is the velocity at time t, show that 
is constant of the motion.
(i) Find E given that initially 
when x=0.
(ii) Find E if initially v=10 where x=0, instead of the result in (i). Describe the motion of the particle.
13. (i) For a particle moving on the x-axis, and distant x from 0 at time t, prove that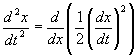 
.
(ii) 
, show that 
does not change with time. Find E given dx/dt =0 where x=1 and hence find an expression for dx/dt in terms of x. Show that the particle is restricted to a certain interval in the line, and describe its motion.
14. The acceleration of a body P is given by 
where x is the displacemnt of P from 0 at time t; the velocity then is v. If t=0, x=0, v=3 and v>0 throughout the motion, find v in terms of x and show that x=tan3t. Determine x, v when t=p/12.
15. A particle moves in a straight line and its acceleration at any time t is given by 
, find dx/dt given that dx/dt=1 when x=0. (ans:
).
16. The acceleration of a body moving towards the earth under gravitational attraction varies inversely as the square of its distance from the centre of the earth. Express as a differential equation and prove that if the body starts from rest at a distance a from the centre of the earth, its speed at x from the centre of the earth is 
, where k is a constant. (ans: 
).
17. A particle moves in a straight line and its acceleration at any time t is 
. If v=1 and x=0 when t=0.
(a) Express its velocity v in terms of x. (ans: 
)
(b) Express its displacement x in terms of time t. (ans: ln(t+1))